Производная функции на C++ часто вычисляется с помощью разнообразных приближенных формул.
Например, есть следующие формулы для приближенного вычисления первой производной функции:
- левая разностная производная
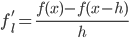, - правая разностная производная
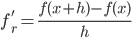, - центральная разностная производная
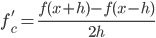, эта формула точнее предыдущих.
Есть также формула для приближенного вычисления второй производной функции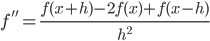 
.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
#include <iostream.h> // подключаем функции ввода/вывода double f(double x) { //здесь функция, производную которой нужно найти, например, x^2 return x * x; } main() { double x, h, fl, fr, fc, f2; x = 1; // точка, в которой вычисляем производную h = 0.1; // шаг, с которым вычисляем производную // приближенно вычисляем первую производную различными способами fl = (f(x) - f(x - h)) / h; // левая fr = (f(x + h) - f(x)) / h; // правая fc = (f(x + h) - f(x - h)) / (2 * h); // центральная // приближенно вычисляем вторую производную f2 = (f(x + h) - 2 * f(x) + f(x - h)) / (h * h); // выводим результаты на экран cout<<"x = "<<x<<"\n"; cout<<"fl = "<<fl<<"\n"; cout<<"fr = "<<fr<<"\n"; cout<<"fc = "<<fc<<"\n"; cout<<"f2 = "<<f2<<"\n"; system("pause"); } |
Более сложный, но учитывающий различные особенности вычисления производных код можно найти в какой-нибудь стандартной программе для вычисления производной или какой-нибудь библиотеке численных методов.
